数学が苦手な子必見!図形問題が得意になる勉強法

新松戸のプリモ個別指導塾 石垣です。図形問題は公式や定理を覚えることだけではなく、問題によってどの公式・定理を用いればよいのかがわからないとちょっとした応用問題すら理解不能になってしまいいます。私が以前勤めていた学習塾に理系の最高峰、東工大の方に講師として来ていただいていたのですが、彼曰く、「図形はセンスです。」と言っていました。それほどどの公式・定理を当てはめるのかという部分は難しいところでもあります。しかし中学校・公立高校の入試レベルの問題であれば、勉強のやり方次第で充分解けるようになります。図形問題の勉強法のコツをご紹介したいと思います。
図形問題を解けるようになるコツ
1. 公式・定理をしっかり暗記する
あなたは図形の面積を求める公式や三角形の合同条件、三平方の定理等、公式・定理をしっかり覚えていますか?学年別で、覚えておくべきことを書いておきます。
【中学1年生】
中1では図形の基礎を学びます。公式・定理というよりは、用語・記号をしっかり覚えましょう。また公式については小学校で習った形ではなく、文字式による公式の表し方をしっかり覚えましょう。
【中学2年生】
中2では本格的な図形問題に入ります。対頂角・同位角・錯角の関係、三角形の合同条件、証明の手順、各図形の定義は、必ず覚えておきましょう。
【中学3年生】
中3ではより深く図形問題を解いていくことになります。三角形の相似条件、三角形の線分の比の使い方、中点連結定理、相似比と面積比・体積比の関係、円周角の定理、三平方の定理まではしっかり覚えましょう。余裕があればメラニウスの定理まで覚えましょう。
公式・定理を覚えて、それを問題にどうやって使っていくかが図形問題の基本の解き方ですので、これらを暗記しておくことがまずは必須です。
図形問題を解くカギは補助線
図形問題を解くカギは出題された図形に「補助線」を引くことです。補助線を引くことによって、どの公式、定理を使ってよいのかが見えてきます。例えば中1の問題を題材にご紹介します。この問題は某中学校の2学期期末テストに実際に出題されたものです。
Q. 1辺12㎝の正方形の中に書かれた図形のうち、斜線部分の面積を求めなさい。
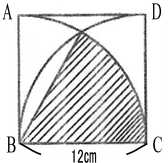
この問題では斜線部のおうぎ形の半径(r)は12㎝だということはすぐにわかります。あとは中心角なのですがこれがこの図を見ただけではすぐにわかりません。ところが、先程説明した「補助線」を引くとこうなります。

正方形の頂点Cから弧ACと弧BDの交点をEとすると、そのEに向かって直線を自分で引いてみます。すると、斜線部おうぎ形だけでなく弧をBEとするおうぎ形CBAと、正方形の辺BCを一辺とする三角形BCEができます。斜線部おうぎ形の半径はBCとBE、BEを弧とするするおうぎ形の半径はBCとEC、BCが共通なので、BC=BE=ECと言えます。つまり補助線を引いたことによってできた三角形BCEは1辺12㎝の正三角形であることがわかります。斜線部おうぎ形の中心角∠CBEは三角形BCEの内角です。三角形BCEは正三角形なので内角はどれも60度。斜線部おうぎ形の中心角は60度であることがわかります。あとはおうぎ形の面積のaに60を代入して答えを求めればよいわけです。答えは24π㎠とわかります。
このように図形問題は、補助線を自分で引くことで解答を導き出せる問題なのです。
補助線をどこに引く?
補助線を引けと言われてもどこに引けばよいかわからない。という人は次の2つの考え方を頭に入れておいてください。
◎与えられた情報を利用するために引く
◎必要な情報を探し出すために引く
です。この2つの視点をどういう時に使えばよいのかがわかるには、色々な問題を解いていくしかありません。図形の勉強は1冊の問題集を完璧にするという反復演習よりも、ある程度、色々な問題集を使って数多くのパターンを演習した方が良いと思います。また各問題についてわからないようであれば、何分も考え込むより、解答の解説を読みながら解き方を覚え、自分で改めてその問題を解いてみるという風に勉強してみてください。ですから問題集を選ぶ時には、解答・解説が充実しているものを選びましょう。もちろん解説を読んで補助線を引いてあるのならば、これは上記2つの考え方のどちらで引いたのだろうという疑問を持ちながら学習してください。